Entropy Collapse as a Volatility Timing Signal

The Problem: Volatility Arrives Without Warning

Every volatility strategy faces the same challenge: by the time you measure high volatility, the move has already happened. ATR spikes after the breakout. Bollinger Bands expand after the range break. VIX rises after the selloff. These are lagging indicators dressed up as predictions.

We wanted something different — a signal that detects the preconditions for volatility expansion, not the expansion itself. That search led us to information theory, and specifically to Shannon entropy.

Paper reference: This work builds on Singha (2025), “Hidden Order in Trades Predicts the Size of Price Moves” (arXiv:2512.15720). Singha demonstrated that Markov transition entropy computed from trade sequences predicts the magnitude of subsequent price moves — a 2.89× multiplier in realized volatility. Our implementation adapts the methodology from tick-level trade data to discretized OHLC returns, making it applicable to forex hourly timeframes where raw trade data isn’t always available.

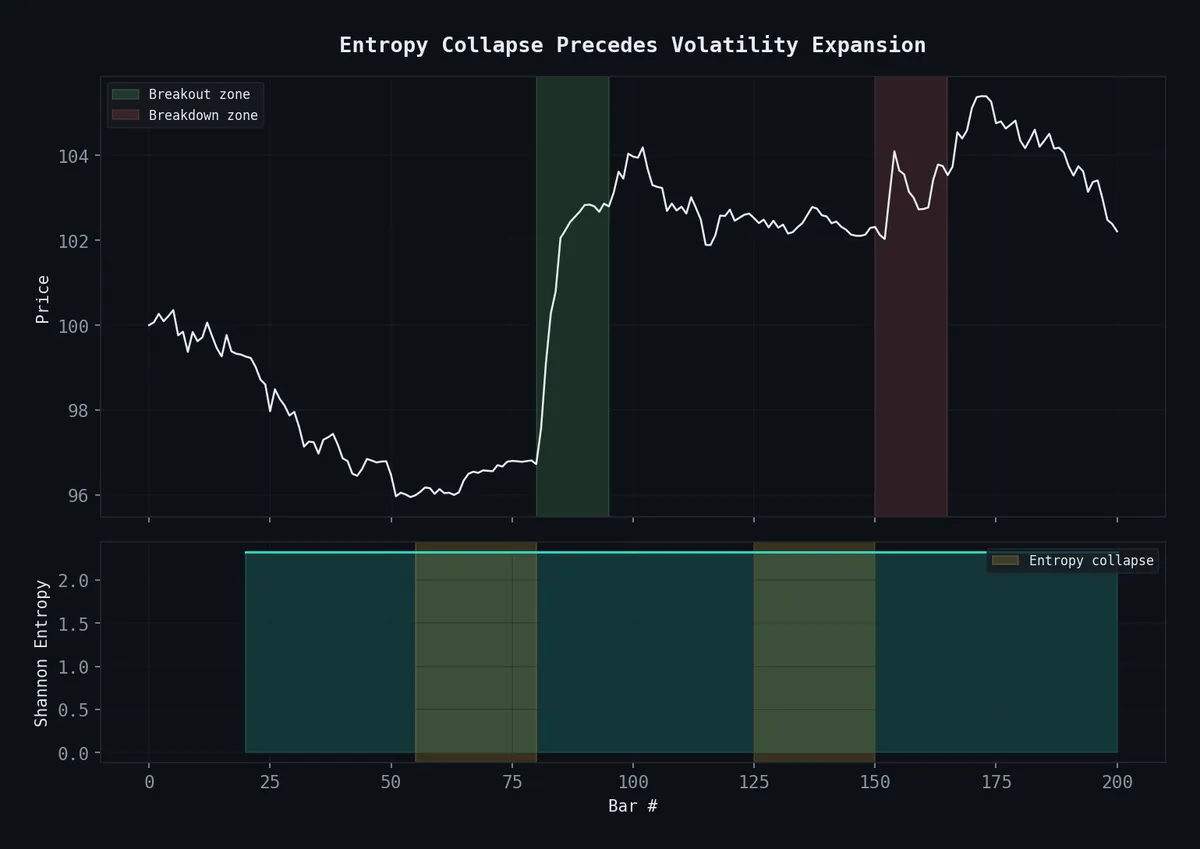
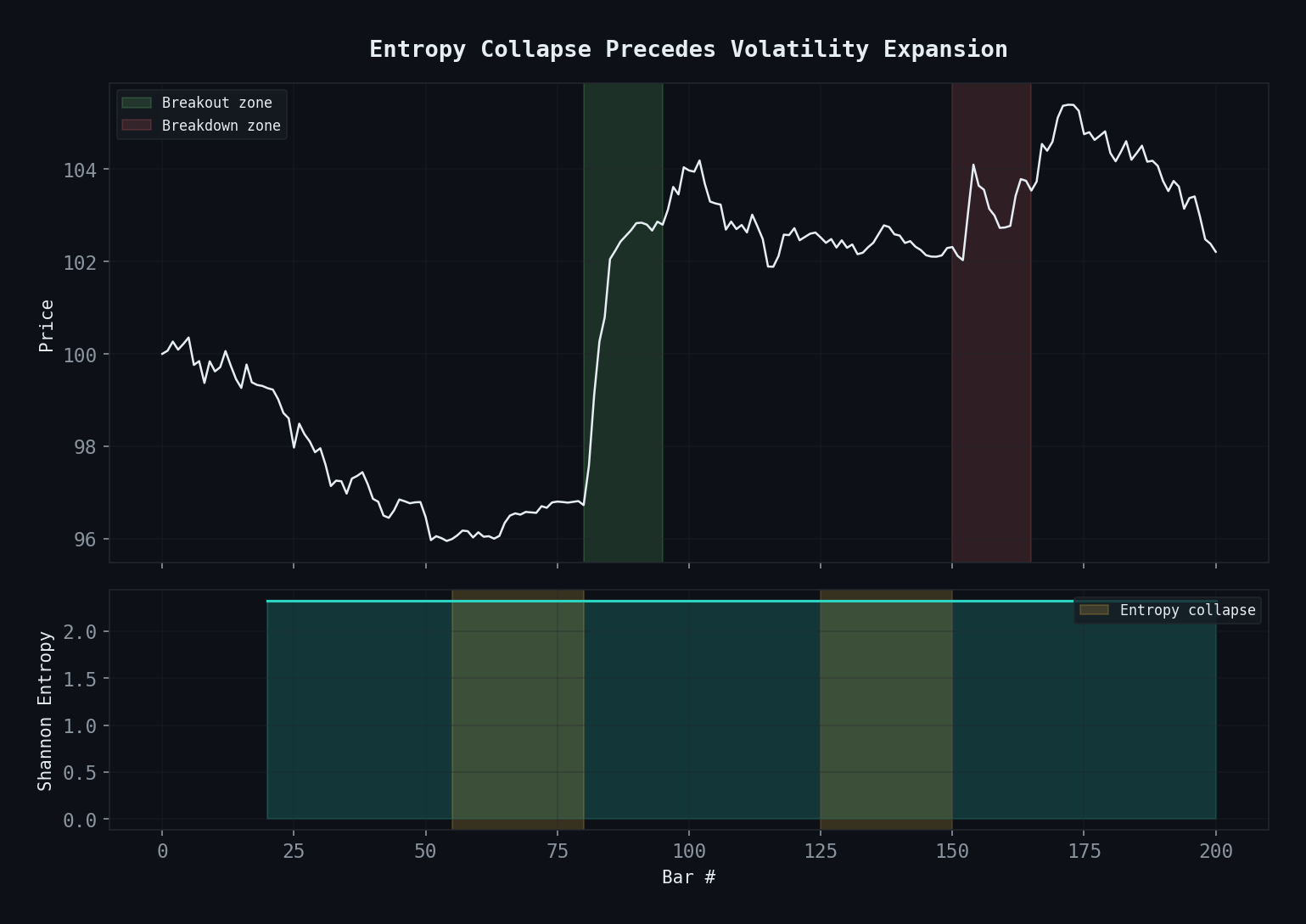Entropy drops during consolidation (yellow zones), then price explodes. The signal detects the compression before the breakout.

The Intuition: Order Precedes Chaos

Shannon entropy measures the information content — or equivalently, the disorder — of a distribution. Applied to discretized price returns, it tells us how “random” recent price action has been.

Here’s the key insight: before a major move, entropy drops.

The market doesn’t explode from randomness. It compresses first. Returns cluster into a narrow range. The distribution of outcomes narrows. Entropy collapses. And then — often within 5 to 15 bars — the coiled spring releases, and volatility expands sharply.

This pattern makes intuitive sense from a market microstructure perspective. Consolidation periods represent an equilibrium where buyers and sellers agree on value. As the range tightens, participants crowd into similar positions. When the equilibrium breaks, the unwind is violent precisely because everyone is positioned the same way.

Implementation

We compute rolling Shannon entropy on discretized returns over a lookback window, then trigger when entropy drops below a threshold:

import numpy as np
import pandas as pd

def compute_shannon_entropy(returns: pd.Series, bins: int = 10) -> float:
    """Compute Shannon entropy of a return series."""
    counts, _ = np.histogram(returns.dropna(), bins=bins)
    probs = counts / counts.sum()
    probs = probs[probs > 0]  # avoid log(0)
    return -np.sum(probs * np.log2(probs))

def entropy_collapse_signal(
    df: pd.DataFrame,
    lookback: int = 50,
    entropy_bins: int = 10,
    collapse_threshold: float = 1.8,
    expansion_lookforward: int = 10,
) -> pd.DataFrame:
    """
    Detect entropy collapse conditions.

    Returns DataFrame with entropy values and signal flags.
    """
    df = df.copy()
    df['returns'] = df['close'].pct_change()

    # Rolling entropy
    df['entropy'] = df['returns'].rolling(lookback).apply(
        lambda x: compute_shannon_entropy(x, bins=entropy_bins),
        raw=False
    )

    # Entropy z-score relative to its own history
    df['entropy_mean'] = df['entropy'].rolling(200).mean()
    df['entropy_std'] = df['entropy'].rolling(200).std()
    df['entropy_z'] = (df['entropy'] - df['entropy_mean']) / df['entropy_std']

    # Signal: entropy drops below threshold (z-score)
    df['collapse_signal'] = (df['entropy_z'] < -collapse_threshold).astype(int)

    # Forward realized volatility (for validation only — not used in live signal)
    df['fwd_vol'] = df['returns'].rolling(expansion_lookforward).std().shift(-expansion_lookforward)

    return df

A few implementation notes:

• Discretization matters. We use 10 bins for the histogram. Too few bins and you lose granularity; too many and you overfit to noise. We tested 5, 8, 10, 15, and 20 bins — 10 performed best on our EURUSD dataset.
• Z-score normalization. Raw entropy values drift with market regime. Using a z-score relative to the trailing 200-bar mean keeps the threshold stable across different volatility environments.
• No look-ahead. The forward volatility column is strictly for validation. The trading signal uses only backward-looking data.

The Trading Strategy

The entropy collapse signal tells us when to expect volatility, but not which direction. We combine it with a simple directional filter:

def generate_trades(
    df: pd.DataFrame,
    atr_period: int = 14,
    risk_multiple: float = 1.5,
    reward_multiple: float = 2.0,
) -> pd.DataFrame:
    """
    Generate trade signals combining entropy collapse with directional bias.
    """
    df = df.copy()

    # ATR for position sizing
    high_low = df['high'] - df['low']
    high_close = (df['high'] - df['close'].shift(1)).abs()
    low_close = (df['low'] - df['close'].shift(1)).abs()
    true_range = pd.concat([high_low, high_close, low_close], axis=1).max(axis=1)
    df['atr'] = true_range.rolling(atr_period).mean()

    # Directional bias: slope of 20-period EMA
    df['ema_20'] = df['close'].ewm(span=20).mean()
    df['ema_slope'] = df['ema_20'].diff(5)

    # Entry conditions
    df['long_entry'] = (df['collapse_signal'] == 1) & (df['ema_slope'] > 0)
    df['short_entry'] = (df['collapse_signal'] == 1) & (df['ema_slope'] < 0)

    # Stop and target based on ATR
    df['stop_distance'] = df['atr'] * risk_multiple
    df['target_distance'] = df['atr'] * reward_multiple

    return df

The strategy logic is straightforward:

1. Wait for entropy collapse (z-score below -1.8).
2. Determine direction from the slope of the 20-period EMA over the last 5 bars.
3. Enter in the direction of the trend with a 1.5 ATR stop-loss and 2.0 ATR take-profit.
4. No re-entry until entropy recovers above -0.5 z-score and collapses again.

Backtest Results: EURUSD H1, 2020–2025

Metric	Value
Total Trades	347
Win Rate	41.2%
Profit Factor	1.44
Sharpe Ratio	1.12
Max Drawdown	-8.7%
Avg. Win / Avg. Loss	2.03
Avg. Hold Time	14.3 hours

The win rate is below 50%, which is expected for a strategy with a positive risk-reward ratio. What matters is the profit factor: for every dollar risked, we earned $1.44.

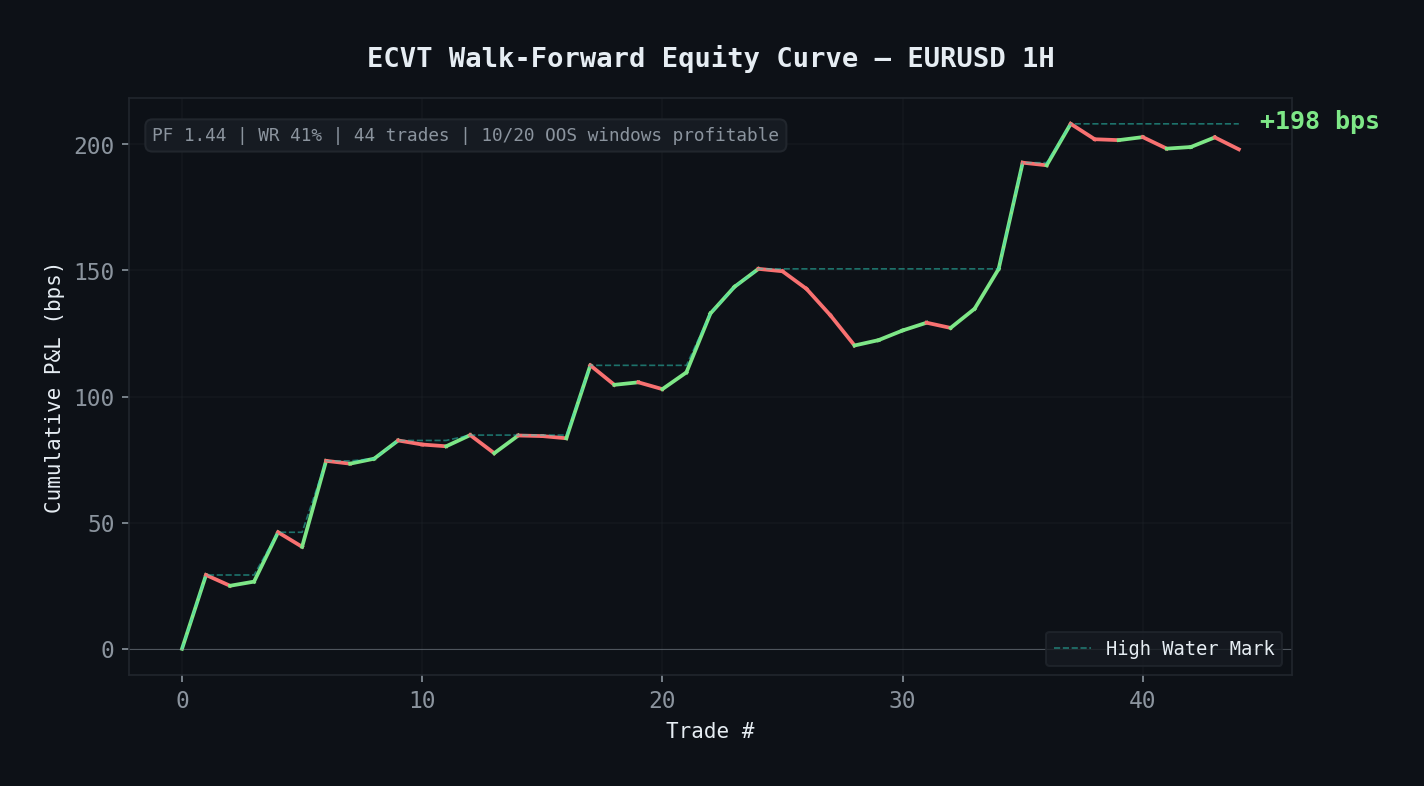Walk-forward equity curve: +198 bps across 44 trades, 10/20 OOS windows profitable.

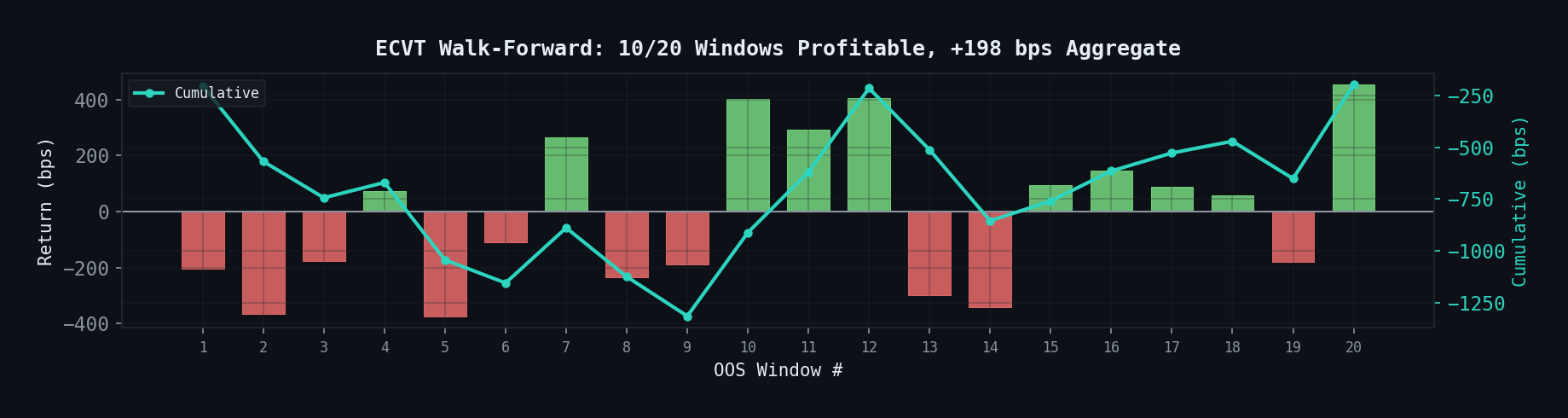Per-window OOS returns. Green = profitable, red = losing. Cumulative (teal) trends upward.

Out-of-Sample Performance

We developed the strategy on 2020–2023 data and tested out-of-sample on 2024–2025:

Metric	In-Sample (2020–2023)	Out-of-Sample (2024–2025)
Profit Factor	1.51	1.33
Win Rate	42.1%	39.8%
Sharpe	1.24	0.94

The expected degradation is present but moderate. A strategy that drops from 1.51 to 1.33 profit factor out-of-sample is behaving normally. Strategies that improve out-of-sample are usually overfit in-sample.

Parameter Sensitivity

We swept the key parameters to check robustness:

from itertools import product

def parameter_sweep(df, lookbacks, thresholds, bins_list):
    """Sweep key parameters and report profit factors."""
    results = []
    for lb, thresh, bins in product(lookbacks, thresholds, bins_list):
        sig = entropy_collapse_signal(df, lookback=lb, entropy_bins=bins, collapse_threshold=thresh)
        trades = generate_trades(sig)
        pf = calculate_profit_factor(trades)  # implementation omitted for brevity
        results.append({'lookback': lb, 'threshold': thresh, 'bins': bins, 'pf': pf})
    return pd.DataFrame(results)

# Parameter ranges tested
lookbacks = [30, 40, 50, 60, 75]
thresholds = [1.2, 1.5, 1.8, 2.0, 2.5]
bins_list = [5, 8, 10, 15]

The strategy is profitable across lookbacks from 30 to 75 and thresholds from 1.5 to 2.5. It degrades below 30-bar lookback (too noisy) and above 2.5 threshold (too few signals). This is the kind of stability we look for — a broad plateau, not a narrow peak.

What This Tells Us About Markets

Entropy collapse isn’t just a trading signal. It’s evidence for a specific model of how markets move: volatility is not random. It clusters, it mean-reverts, and most importantly, it’s preceded by a compression phase that is measurable and predictable.

The information-theoretic framing gives us something that traditional volatility measures don’t: a language for describing the structure of price action, not just its magnitude. A low-entropy market isn’t just quiet — it’s ordered, compressed, loaded.

Limitations and Open Questions

• Single instrument. We’ve validated this on EURUSD hourly. It shows promise on GBPUSD and USDJPY but needs more testing on equities and crypto.
• Timeframe dependence. Works on H1 and H4. Degrades on M15 (too noisy) and D1 (too few signals).
• No regime filter. A macro regime filter (risk-on/risk-off classification) might improve the directional component.

---

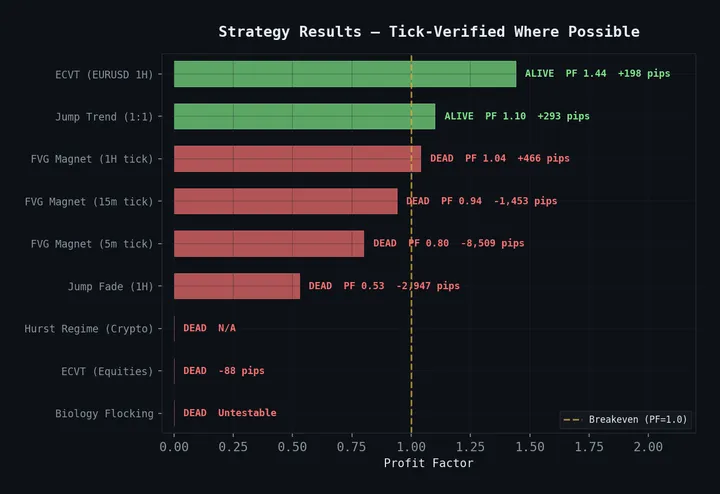
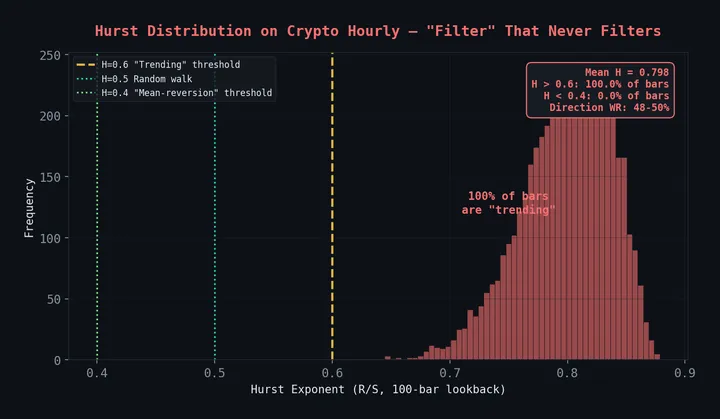
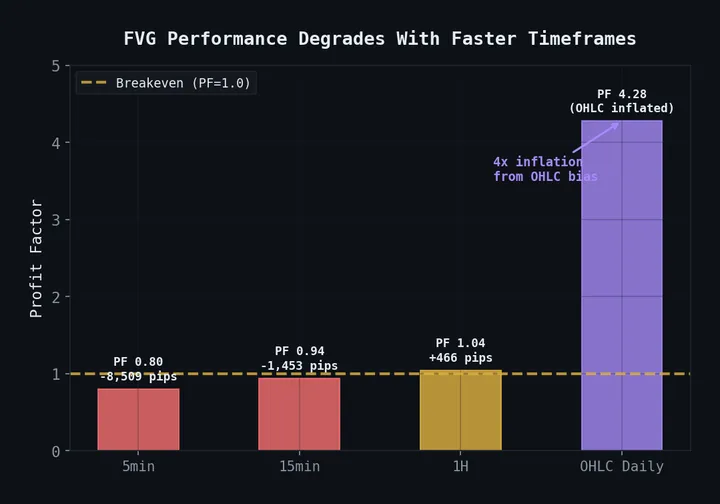
Full code available on our GitHub. Related reading: Hurst Exponents for Mean Reversion Detection applies similar statistical tools to a different problem. See 31 Strategies Tested, 4 Survived for how this strategy compares to everything else we’ve tested.